多目标优化算法的解读

近年来，随着人工智能技术的快速发展，多目标优化算法在推荐系统、物流配送、路径规划等领域得到了广泛应用。本文将从以下几个方面介绍多目标优化算法的问题定义、帕累托解集的定义、多目标优化的经典算法和算法的应用。

## 多目标优化的问题定义

多目标优化问题是指在输入空间中寻找一个或多个解，在满足多个目标函数约束条件的情况下，使得所有目标函数达到最优或接近最优状态的问题。多目标优化算法的目的是在不同的目标函数之间平衡，以获得帕累托前沿（Pareto front）的解集。

## 帕累托解集的定义

帕累托解集是指在多目标优化模型中，所有最优解的集合。这些解被称为“非支配解”，因为它们不被其他解所支配，并且没有其他解在所有目标函数上比其更优。帕累托前沿是帕累托解集的几何表现，是在多维目标函数空间中的所有非支配解构成的集合。

## 多目标优化的经典算法

### 线性加权法（Weighted Sum Method）

线性加权法是一种简单的多目标优化算法，通过将每个目标函数乘以预先定义的适当系数，然后将它们相加来确定一个加权总和作为目标函数。该方法能够确定一个解，但不能确定帕累托前沿上的所有解。

### 主要目标法（Objective Programming Method）

主要目标法旨在找到一个使多个目标函数中最相关的目标函数最优化的解。在这种方法中，将所有目标函数视为一个整体来最小化或最大化，而把其他目标函数看成约束条件，这样就得到了主要目标函数的最优解。

### 粒子群算法（Particle Swarm Optimization）

粒子群算法是一种基于群体智能的优化技术，用于求解连续空间的优化问题。该算法采用类似于鸟群或鱼群的行为模式，利用种群中的每个个体进行探索和开发，以在多目标问题上获得最优解。

## 多目标优化算法的应用

多目标优化算法的应用非常广泛，包括推荐系统、物流配送、路径规划等领域。其中，推荐系统是应用多目标优化算法最为广泛的领域之一。通过将用户兴趣与物品特征相结合，推荐系统可以提供更准确和个性化的推荐。

在物流配送中，多目标优化算法可以应用于包括货物装载、车辆路径规划、仓库管理等方面，有效减少物流成本并提高效率。

在路径规划领域，多目标优化算法被广泛应用于交通网络规划和机器人路径规划等问题中。多目标优化算法可以有效平衡不同的目标函数，获得更优的解决方案。

## 结论

多目标优化算法是一个重要的优化技术，可以应用于推荐系统、物流配送、路径规划等各种领域。线性加权法、主要目标法和粒子群算法是多目标优化算法中比较常用的算法。能够使用多目标优化算法找到帕累托前沿上的所有解，可以帮助解决复杂的实际问题，提高问题求解的效率和准确性。

霸王龙优化算法（Tyrannosaurus optimization，TROA）由Venkata Satya Durga Manohar Sahu等人于2023年提出，该算法模拟霸王龙的狩猎行为，具有搜索速度快等优势。

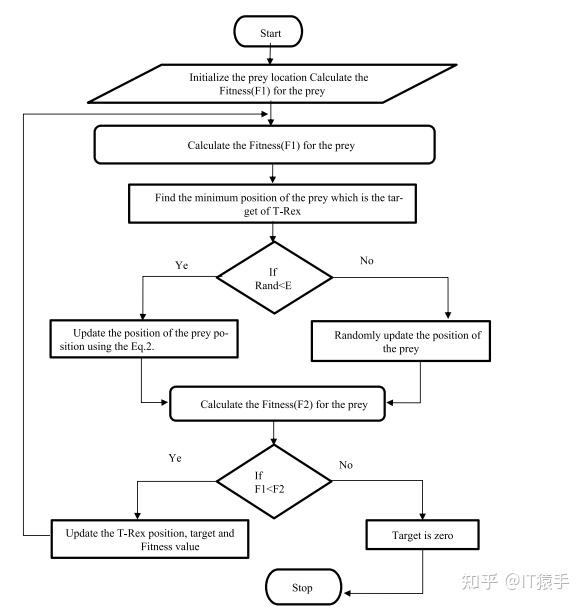
参考文献：Venkata Satya Durga Manohar Sahu, Padarbinda Samal, Chinmoy Kumar Panigrahi,”Tyrannosaurus optimization algorithm: A new nature-inspired meta-heuristic algorithm for solving optimal control problems”,e-Prime - Advances in Electrical Engineering, Electronics and Energy,Volume 5,2023,100243,ISSN 2772-6711,https://doi.org/10.1016/j.prime.2023.100243.

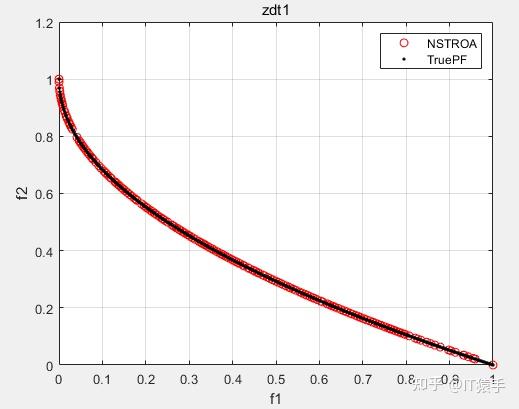
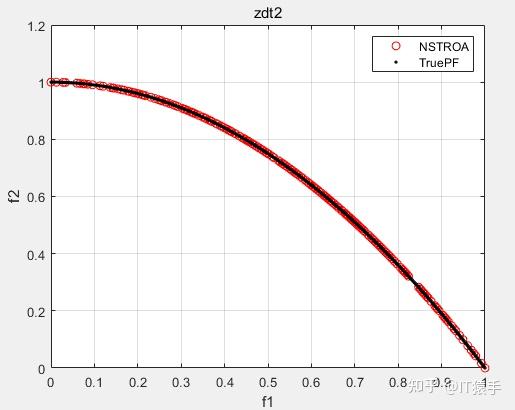
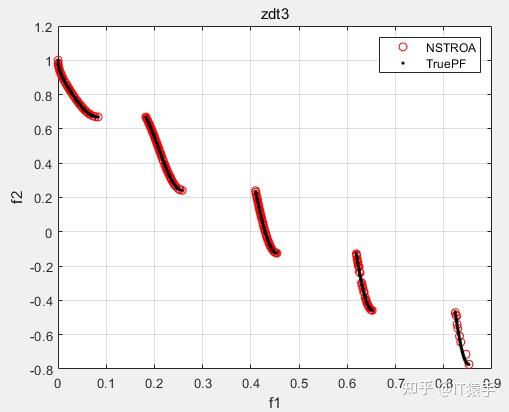
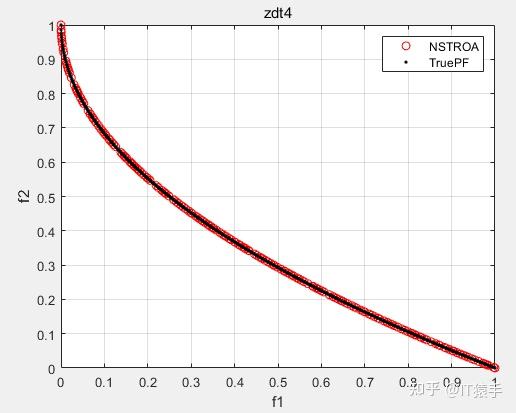
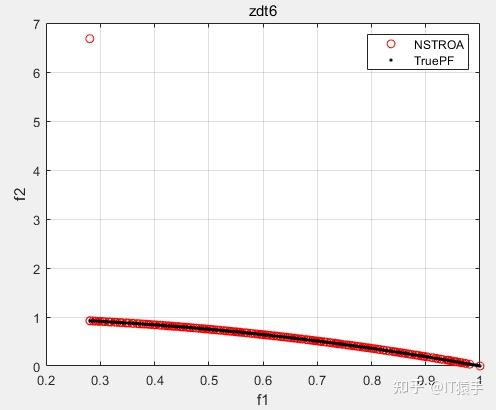
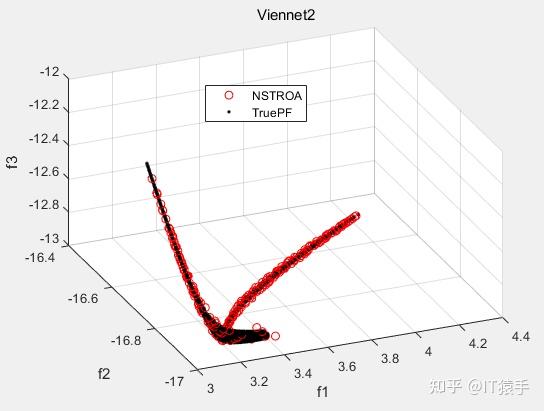
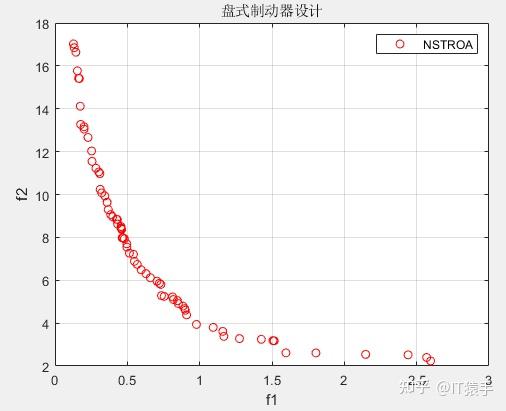
基于非支配排序的霸王龙优化算法（Non-Dominated Tyrannosaurus optimization，NSTROA）由霸王龙优化算法与非支配排序策略结合而成。将NSTROA用于求解46个多目标测试函数（ZDT1、ZDT2、ZDT3、ZDT4、ZDT6、DTLZ1-DTLZ7、WFG1-WFG10、UF1-UF10、CF1-CF10、Kursawe、Poloni、Viennet2、Viennet3）以及1个工程应用（盘式制动器设计）,并采用IGD、GD、HV、SP进行评价。

（1）部分代码

close all;
clear ; 
clc;
%%
% TestProblem测试问题说明：
%一共46个多目标测试函数，详情如下：
%1-5:ZDT1、ZDT2、ZDT3、ZDT4、ZDT6
%6-12：DZDT1-DZDT7
%13-22：wfg1-wfg10
%23-32：uf1-uf10
%33-42：cf1-cf10
%43-46:Kursawe、Poloni、Viennet2、Viennet3
%47 盘式制动器设计 温泽宇,谢珺,谢刚,续欣莹.基于新型拥挤度距离的多目标麻雀搜索算法[J].计算机工程与应用,2021,57(22):102-109.
%%
TestProblem=1;%1-47
MultiObj=GetFunInfo(TestProblem);
MultiObjFnc=MultiObj.name;%问题名
% Parameters
params.Np=100;        % Population size
params.Nr=200;        % Repository size
params.maxgen=100;    % Maximum number of generations
numOfObj=MultiObj.numOfObj;%目标函数个数
D=MultiObj.nVar;%维度
f=NSTROA(params,MultiObj);
X=f(:,1:D);%PS
Obtained_Pareto=f(:,D+1:D+numOfObj);%PF
if(isfield(MultiObj,'truePF'))%判断是否有参考的PF
True_Pareto=MultiObj.truePF;
%%  Metric Value
% ResultData的值分别是IGD、GD、HV、Spacing  (HV越大越好，其他指标越小越好)
ResultData=[IGD(Obtained_Pareto,True_Pareto),GD(Obtained_Pareto,True_Pareto),HV(Obtained_Pareto,True_Pareto),Spacing(Obtained_Pareto)];
else
    %计算每个算法的Spacing，Spacing越小说明解集分布越均匀
    ResultData=Spacing(Obtained_Pareto);%计算的Spacing
end
%%
disp('Repository fitness values are stored in Obtained_Pareto');
disp('Repository particles positions are store in X');

（2）部分结果