99行Matlab拓扑优化程序解析—2 迭代过程

日期：2024-08-26 06:07 | 人气：

本文将针对99行Matlab拓扑优化程序中的迭代过程代码进行介绍，以帮助读者理解程序的迭代计算过程。

% START ITERATION（开始迭代）
while change > 0.01         %%当伪密度变化小于0.01时停止 
  loop = loop + 1;          %%迭代次数+1
  xold = x;                 %%储存当前密度值
% FE-ANALYSIS（有限元分析）
  [U]=FE(nelx,nely,x,penal);        %%调用有限元分析函数,返回整体位移矩阵U        
% OBJECTIVE FUNCTION AND SENSITIVITY ANALYSIS（目标函数和灵敏度分析）
  [KE] = lk;                        %%获取单元刚度矩阵KE,各单元均相同
  c = 0.;                           %%初始化柔顺度
  for ely = 1:nely
    for elx = 1:nelx
      n1 = (nely+1)*(elx-1)+ely;    %%计算左上节点编号n1
      n2 = (nely+1)* elx   +ely;    %%计算右上节点编号n2
      Ue = U([2*n1-1;2*n1; 2*n2-1;2*n2; 2*n2+1;2*n2+2; 2*n1+1;2*n1+2],1); %%提取单元上各节点的位移
      c = c + x(ely,elx)^penal*Ue'*KE*Ue;                                 %%计算柔顺度
      dc(ely,elx) = -penal*x(ely,elx)^(penal-1)*Ue'*KE*Ue;                %%计算灵敏度
    end
  end
% FILTERING OF SENSITIVITIES（灵敏度过滤）
  [dc]   = check(nelx,nely,rmin,x,dc); %%调用网格过滤函数,返回过滤后的灵敏度   
% DESIGN UPDATE BY THE OPTIMALITY CRITERIA METHOD（优化准则法求解）
  [x]    = OC(nelx,nely,x,volfrac,dc); %%利用优化准则法优化设计变量
% PRINT RESULTS（输出结果）
  change = max(max(abs(x-xold)));      %%更新伪密度变化
  disp([' It.: ' sprintf('%4i',loop) ' Obj.: ' sprintf('%10.4f',c) ...
       ' Vol.: ' sprintf('%6.3f',sum(sum(x))/(nelx*nely)) ...
        ' ch.: ' sprintf('%6.3f',change )])                                  %%输出
% PLOT DENSITIES（绘制优化结果）
  colormap(gray); imagesc(-x); axis equal; axis tight; axis off;pause(1e-6); %%绘图
end
  1. 迭代控制
while change > 0.01
  loop = loop + 1;

每一轮迭代开始前，先对循环控制器change进行检查。当循环控制器值小于等于求解精度0.01时，终止迭代。

若循环控制器值大于0.01，即未达到求解精度，则进入下一轮的迭代过程继续求解。同时，迭代计数器loop中存储的迭代次数加一。

2. 有限元分析（详见后续对应子程序解读）

[U]=FE(nelx,nely,x,penal);

调用有限元分析子程序，将单元网格、伪密度矩阵（首次迭代为初始伪密度矩阵，迭代过程中为上一轮迭代得到的伪密度矩阵）、惩罚因子传递给子程序进行分析，得到并返回一个整体位移矩阵。

3. 获取单元刚度矩阵（详见后续对应子程序解读）

[KE] = lk;

根据材料属性（子程序内置）弹性模量和泊松比，求出单元刚度矩阵。各单元刚度矩阵一致。

4. 柔顺度及灵敏度计算

c = 0.;

初始化整体柔顺度为0，类型为浮点型小数。

for ely = 1:nely
  for elx = 1:nelx
      ......
  end
end

遍历（行优先）全部单元。

n1 = (nely+1)*(elx-1)+ely;
n2 = (nely+1)* elx   +ely;
Ue = U([2*n1-1;2*n1; 2*n2-1;2*n2; 2*n2+1;2*n2+2; 2*n1+1;2*n1+2],1);

对于每一个单元，以左上和右上两个节点编号为基准，从整体位移矩阵中提取该单元的位移矩阵。

图1 单元节点及自由度编号

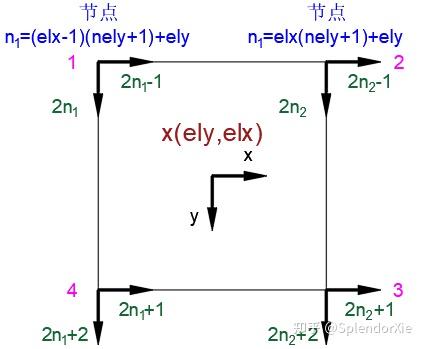
对于每个单元的四个节点，它们的内部节点编号按顺时针顺序排布，单元的位移矩阵为：

\\[{{\\rm{U}}_{\\rm{e}}}={\\left[{\\begin{array}{*{20}{c}}{{u_1}}&{{v_1}}&{{u_2}}&{\\begin{array}{*{20}{c}}{{v_2}}&{{u_3}}&{{v_3}}&{\\begin{array}{*{20}{c}}{{u_4}}&{{v_4}}\\end{array}}\\end{array}}\\end{array}}\\right]^{\\rm{T}}}\\]

\\[{{u_i}}\\] 和 \\[{{v_i}}\\] (i=1, 2, 3, 4)表示对应内部节点处的X方向和Y方向的位移。

c = c + x(ely,elx)^penal*Ue'*KE*Ue;

根据应变能公式 \\[c\\left({\\rm{x}}\\right)={{\\rm{U}}^T}{\\rm{KU}}=\\sum\\limits_{e=1}^N{{{\\left({{x_e}}\\right)}^p}}{\\rm{u}}_e^T{{\\rm{k}}_0}{{\\rm{u}}_e}\\] 计算总应变能。

dc(ely,elx) = -penal*x(ely,elx)^(penal-1)*Ue'*KE*Ue;

根据单元柔顺度公式 \\[\\frac{{\\partial c}}{{\\partial{x_e}}}=- p{\\left({{x_e}}\\right)^{p - 1}}{\\rm{u}}_e^T{{\\rm{k}}_0}{{\\rm{u}}_e}\\] 计算每个单元的柔顺度。

5. 灵敏度过滤（详见后续对应子程序解读）

[dc] = check(nelx,nely,rmin,x,dc);

调用灵敏度过滤子程序，将单元网格、过滤半径、伪密度矩阵、柔顺度矩阵传递给子程序进行灵敏度过滤，得到并返回新的灵敏度矩阵。

6. 优化准则法求解（详见后续对应子程序解读）

[x] = OC(nelx,nely,x,volfrac,dc);

调用OC算法子程序，将单元网格、伪密度矩阵、体分比、过滤后的柔顺度矩阵传递给子程序进行求解，得到并返回新的伪密度矩阵。

7. 后处理

change = max(max(abs(x-xold)));

计算所有单元伪密度变化（相对上一轮迭代，第一轮迭代时相对初始伪密度）的最大值，并更新循环控制器。

disp([' It.: ' sprintf('%4i',loop) ' Obj.: ' sprintf('%10.4f',c) ...
      ' Vol.: ' sprintf('%6.3f',sum(sum(x))/(nelx*nely)) ...
      ' ch.: ' sprintf('%6.3f',change )])
colormap(gray); imagesc(-x); axis equal; axis tight; axis off;pause(1e-6);

输出结果。

如有不当的地方，欢迎指正！

利盈资讯

旋转小火锅定制流程

免费咨询

提供图纸

免费设计

免费报价

无忧安装

终身维护

平台注册入口