模型优化
日期:2024-09-09 13:16 | 人气:
优化是应用数学的一个分支,也是机器学习的核心组成部分。实际上,机器学习算法 = 模型表征 + 模型评估 + 模型优化。其中,模型优化所做的事情就是在模型表征空间(假设空间)中找到模型评估指标最好的模型。需要注意的是不同的优化算法对应的模型表征和评估指标不尽相同。
先前,我很纠结是把损失函数放在模型评估中,还是放在模型优化这一篇博客中。准确地说,损失函数是用来作为模型评估的标准,不同的模型有不同的损失函数,例如逻辑回归使用交叉熵损失函数,线性回归使用均方误差损失函数。我们统计模型的损失,从而评估模型的优劣。因此,损失函数放到模型评估中是顺理成章的事情。但是,损失函数在模型优化中同样起到非常重要的作用。
很少有模型从一开始就是完美的,我们需要不断地优化模型,让模型逐渐达到理论最优值,而我们优化的目标就是损失函数——让损失函数达到最小值。从这角度来讲,将损失函数放到模型优化中似乎也非常有道理,因此我最终还是将损失函数放到模型优化这一篇博客中。
在本篇博客中除了讲述损失函数外,还包括机器学习中经典的优化算法、模型调参等相关知识,内容主要来源于博主阅读的书籍以及博主的个人领悟,若有偏驳之处,还望指出。
不严谨地讲,凸优化是指在标准优化问题的范畴内,要求目标函数和约束函数是凸函数的一类优化问题。凸优化是一个很广且复杂的领域,在此仅仅只作简单的介绍。
在介绍凸优化前需要先弄明白什么是凸函数。国内外教材关于凸函数和凹函数的定义不同,在查阅资料时需要细心区别。凸函数的严格定义为:函数 L 是凸函数,当且仅当对定义域中的任意两点 x, y 和任意实数
λ
∈
[
0
,
1
]
\lambda \in [0, 1]
λ∈[0,1] 总有
L
(
λ
x
+
(
1
?
λ
)
y
)
≤
λ
L
(
x
)
+
(
1
?
λ
)
L
(
y
)
L(\lambda x + (1 - \lambda)y) \leq \lambda L(x) + (1 - \lambda)L(y)
L(λx+(1?λ)y)≤λL(x)+(1?λ)L(y)
该不等式的一个直观解释是,凸函数曲面上任意两点连接而成的线段,上面任意一点都不会处于该函数曲面的下方,见下图。

那么如何判断一个函数是凸函数呢?最简单的方法是判断当前函数的二阶导数 f’’ 是否大于等于 0,若 f ′ ′ ≥ 0 f'' \geq 0 f′′≥0 则 f 是凸函数,当且仅当 f ′ ′ > 0 f'' > 0 f′′>0,f 是严格凸函数。
后面要讲的平方误差损失函数 L ( f , y ) = ( f ? y ) 2 L(f, y) = (f - y)^2 L(f,y)=(f?y)2 就是一个严格凸函数,我们将其展开 f 2 ? 2 f y + y 2 f^2 - 2fy + y^2 f2?2fy+y2,对 f 求二次导数,最终可得 2,2 > 0,因此平方误差损失函数是一个严格凸函数。
除了借助原函数的二阶导数外,另外一种方法是判断目标函数的二阶 Hessian 矩阵来验证凸性。那么问题来了,怎么求目标函数的二阶 Hessian 矩阵?如何通过二阶 Hessian 矩阵来判断凸性?
- 目标函数的二阶 Hessian 矩阵可通过对目标函数的二阶求导获得,令二阶 Hessian 矩阵为 H。
- 如果 Hessian 矩阵满足半正定的性质 ∑ i = 1 n H i ≥ 0 \sum_{i=1}^nH_i \geq 0 ∑i=1n?Hi?≥0(半正定矩阵的行列式非负),函数为凸函数。
对比这两种方法,可以发现第一种方法针对实数 X,而第二种方法针对向量 X。关于半正定矩阵的内容可以参考这篇文章 浅谈「正定矩阵」和「半正定矩阵」
根据凸优化的不严谨定义,我们知道凸优化处理的目标函数和约束函数是凸函数,而凸函数的局部极小值都是全局最小值,因此我们在对凸函数求导时,求得的极值都是全局最小值。那么什么是局部极小,什么是全局最小?
在模型优化过程中我们时常会谈到两种“最优”:局部极小(local minimum)和全部最小(global minimum),令 E 表示模型在训练集上的误差,模型的训练过程可看作一个参数寻优过程,即在参数空间中寻找一组最优参数使得 E 最小。
- 局部极小点:参数空间内梯度为零的点,只要其误差函数值小于邻点的误差函数值,就是局部极小点。局部极小点可以有多个。
- 全局最小点:局部极小点中误差函数值最小的点,即为全局最小点。全局最小点只有一个。
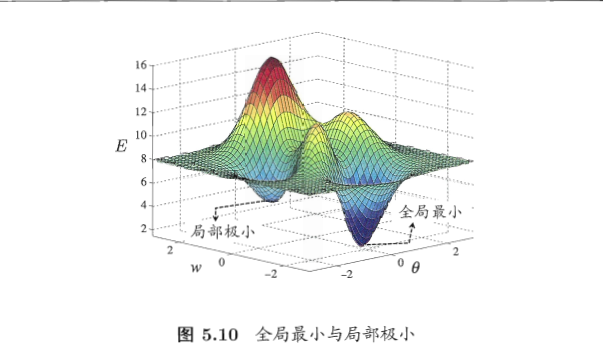
借用下《机器学习》的图,若构成侵权则立即删除。
全局最小点一定是局部极小点,但局部极小点不一定是全局最小点。
那么我们如何找到局部极小点,以及找到全局最小点呢?
【梯度下降算法】:传送门
【随机梯度下降算法】:施工中
损失函数(loss function)用来估量模型预测值与真实值之间的匹配程度,它是一个非负实值函数。损失函数越小,模型的性能以及鲁棒性就越好。
【表示方式】:通常,我们用大写的 L 来表示样本的损失函数。
L
(
y
,
f
(
x
)
)
L(y, f(x))
L(y,f(x))
损失函数是经验风险函数的核心部分,也是结构风险函数重要组成部分。那么什么是经验风险函数?结构风险函数又是什么呢?要阐明经验风险函数以及结构风险函数前,得先介绍风险函数(期望损失)。
我们知道模型的输入、输出 (X, Y) 是随机变量,遵循联合分布 P(X, Y)。例如 X 为年龄, Y 为身高,一般来说身高随着年龄的变化呈现正态分布。令
R
e
x
p
(
f
)
R_{exp}(f)
Rexp?(f) 表示损失函数的期望,则期望的表达式如下:
R
e
x
p
(
f
)
=
E
p
[
L
(
Y
,
f
(
X
)
)
]
=
∫
x
×
y
L
(
y
,
f
(
x
)
)
P
(
x
,
y
)
d
x
d
y
R_{exp}(f) = E_p[L(Y, f(X))] = \int_{x imes y} L(y, f(x))P(x, y)dxdy
Rexp?(f)=Ep?[L(Y,f(X))]=∫x×y?L(y,f(x))P(x,y)dxdy
这是理论上模型 f(X) 关于联合分布 P(X, Y) 平均意义下的损失,称为风险函数(risk function)或期望损失(expected loss)。
但是通常情况下,实际与理论存在差异:很少有数据集完美地符合理论上的分布,或多或少都会存在噪声、异常值,使得数据集与理论的分布存在一定的偏移。而这种非理论的,我们一般称之为经验,所以基于实际数据集的损失函数被称为经验风险函数,用于区分风险函数。下面,我们再用正规的数学语言来定义经验风险函数。
一般地,给定一个训练数据集
T
=
{
(
x
1
,
y
1
)
,
(
x
2
,
y
2
)
,
…
,
(
x
N
,
y
N
)
}
T = \{(x_1, y_1), (x_2, y_2), \ldots, (x_N, y_N)\}
T={(x1?,y1?),(x2?,y2?),…,(xN?,yN?)}
模型 f(X) 关于训练数据集的平均损失称为经验风险(empirical risk)或经验损失(empirical loss),记作
R
e
x
p
R_{exp}
Rexp?,而 f(X) 本身则被称为经验风险函数。
R
e
m
p
(
f
)
=
1
N
∑
i
=
1
N
L
(
y
i
,
f
(
x
i
)
)
R_{emp}(f) = \frac{1}{N}\sum_{i=1}^NL(y_i, f(x_i))
Remp?(f)=N1?i=1∑N?L(yi?,f(xi?))
期望风险 R e x p ( f ) R_{exp}(f) Rexp?(f) 是模型关于联合分布的期望损失,经验风险 R e m p ( f ) R_{emp}(f) Remp?(f) 是模型关于训练样本集的平均损失。根据大数定律,当样本容量 N 趋于无穷时,经验风险 R e m p ( f ) R_{emp}(f) Remp?(f) 趋于期望风险 R e x p ( f ) R_{exp}(f) Rexp?(f)。这也是机器学习所需数据量大的原因之一,数据量越大,则噪声对于整体的影响就会小很多,从而使得训练数据集尽可能贴合真实的数据分布情况。
但需要注意的是,经验风险能取得效果的前提是数据量足够大,如果此时的数据量不够大,那么会发生什么?试想这样一种情形,假设某个数据集符合正态分布,你从该数据集中获取到了一部分数据,而这部分数据恰好都处于正态分布的一侧,然后你用这部分数据去训练模型,接着用剩余的数据集来做测试,最终发现错误率非常高。
原因也非常简单,因为数据量过小,且这部分数据不具有代表性,不能代表整个数据集。此外,数据量过小还会导致模型过度拟合,产生过拟合现象,这怎么理解呢?比如 A 告诉你喝酒是不对的,因为只有 A 告诉过你,所以你很相信 A 说的话,一直认为喝酒是不对的(模型拟合得太好了)。之后你遇到了 B,B 告诉你喝酒可以消愁,是正确的事情,那么你就会开始犹豫,到底喝酒是正确还是不正确?最后你得出了一个结论,视情况而定,在不同的情境下得到的答案也不同。模型训练的过程也是如此,如果数据量过小,模型掌握的知识不够多就有很大概率做出错误的决策。当数据量增加时,模型掌握的知识也越丰富,那么做出正确决策的概率也会随之增加。
正是基于上述原因,为了防止过拟合,结构风险(structural risk)应运而生,在经验风险上加上表示模型复杂度的正则化项(regularizer)或罚项(penalty term)。
R
s
r
m
=
1
N
∑
i
=
1
N
L
(
y
i
,
f
(
x
i
;
θ
)
+
λ
J
(
f
)
)
R_{srm} = \frac{1}{N}\sum_{i=1}^N L(y_i, f(x_i; heta) + \lambda J(f))
Rsrm?=N1?i=1∑N?L(yi?,f(xi?;θ)+λJ(f))
其中,J(f) 表示模型的复杂度。模型 f 越复杂,复杂度 J(f) 就越大;反之,模型 f 越简单,复杂度 J(f) 就越小。也就是说,复杂度表示了对模型的惩罚。
λ
≥
0
\lambda \geq 0
λ≥0 是系数,用以权衡经验风险和模型复杂度。
此时我们的任务就转变为:在保证经验风险足够小的同时也确保结构风险足够小。假如有两个模型 A 和 B,它们的经验风险相差不大 A 略小于 B,但 A 的结构风险远大于 B,此时我们应选择 B 而非 A。奥卡姆剃刀原理也可以说明这一点。
有监督学习的损失函数
在有监督学习中,损失函数刻画了模型和训练样本的匹配程度。假设训练样本的形式为 ( x i , y i ) (x_i, y_i) (xi?,yi?),其中 x i ∈ X x_i \in X xi?∈X 表示第 i 个样本点的特征, y i ∈ Y y_i \in Y yi?∈Y 表示该样本点的标签,f 表示 x i x_i xi? 经过模型后的输出。 L ( f , y i ) L(f, y_i) L(f,yi?) 表示当前样本的损失值,L 越小,表明模型在该样本点匹配得越好。
分类问题
以二分类问题为例,Y = {1, -1},因此 fy > 0 表示分类正确,fy < 0 表示分类错误。
【0-1 损失函数】:
s
i
g
n
?
f
(
x
i
,
θ
)
=
y
i
sign \ f(x_i, heta) = y_i
sign?f(xi?,θ)=yi?。
L
0
?
1
(
f
,
y
)
=
1
f
y
≤
0
=
{
1
,
y
≠
f
(
x
)
0
,
y
=
f
(
x
)
L_{0-1}(f, y) = 1_{fy\leq 0} = \begin{cases} 1, \quad y
eq f(x) \\ 0, \quad y = f(x) \end{cases}
L0?1?(f,y)=1fy≤0?={1,y??=f(x)0,y=f(x)?
其中
1
p
1_p
1p? 是指示函数(Indicator Function),当且仅当 P 为真时取值为 1,否则取值为 0。在上述式子中,fy < 0 为真,表示分类错误取值为 1。假设总共有 100 个样本,其中 5 个样本分类错误,那么损失函数的最终取值为 5。
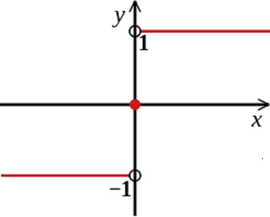
该损失函数能够直观地刻画分类的错误率,但是由于其非凸、非光滑的特点,使得该算法很难直接对该函数进行优化。
【合页(Hinge)损失函数】:
L
h
i
n
g
e
(
f
,
y
)
=
m
a
x
{
0
,
1
?
f
y
}
.
L_{hinge}(f, y) = max\{0, 1-fy\}.
Lhinge?(f,y)=max{0,1?fy}.
Hinge 损失函数是 0-1 损失函数相对紧的凸上界,且当 fy ≥ 1 时,该函数不对其做任何惩罚。Hinge 损失在 fy=1 处不可导,因此不能用梯度下降法进行优化,而是用次梯度下降法(Subgradient Descent Method)。
【Logistic 损失函数】:
L
l
o
g
i
s
t
i
c
(
f
,
y
)
=
l
o
g
2
(
1
+
e
x
p
(
?
f
y
)
)
.
L_{logistic}(f, y) = log_2(1 + exp(-fy)).
Llogistic?(f,y)=log2?(1+exp(?fy)).
Logistic 损失函数也是 0-1 损失函数的凸上界,且该函数处处光滑,因此可以用梯度下降法进行优化。但是,该损失函数对所有的样本点都有所惩罚,因此对异常值相对更敏感一些。
【交叉熵(Cross Entropy)损失函数】:当预测值
f
∈
[
?
1
,
1
]
f \in [-1,1]
f∈[?1,1] 时。
L
c
r
o
s
s
?
e
n
t
r
o
p
y
(
f
,
y
)
=
?
l
o
g
2
(
1
+
f
y
2
)
.
L_{cross \ entropy}(f, y) = -log_2(\frac{1 + fy}{2}).
Lcross?entropy?(f,y)=?log2?(21+fy?).
交叉熵损失函数也是 0-1 损失函数的光滑凸上界。
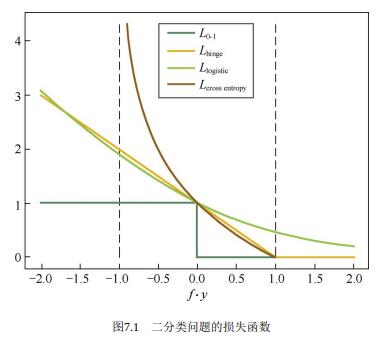
回归问题
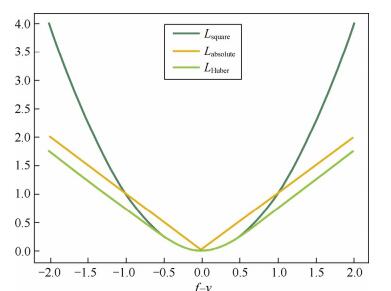
【平方损失函数】:光滑函数,能够用梯度下降发进行优化。但当预测值距离真实值越远时,平方损失函数的惩罚力度越大,因此对异常点比较敏感。
L
s
q
u
a
r
e
(
f
,
y
)
=
(
f
?
y
)
2
L_{square}(f, y) = (f - y)^2
Lsquare?(f,y)=(f?y)2
【绝对损失函数】:对异常点更鲁棒一些,但是,在 f = y 处无法求导数。
L
a
b
s
o
l
u
t
e
(
f
,
y
)
=
∣
f
?
y
∣
L_{absolute}(f, y) = |f - y|
Labsolute?(f,y)=∣f?y∣
【Huber 损失函数】:综合考虑可导性和对异常点的鲁棒性。在 |f - y| 较小时为平方损失,在 |f - y| 较大时为线性损失,处处可导且对异常点鲁棒。
L
H
u
b
e
r
(
f
,
y
)
=
{
(
f
?
y
)
2
,
∣
f
?
y
∣
≤
δ
2
δ
∣
f
?
y
∣
?
δ
2
,
∣
f
?
y
∣
>
δ
L_{Huber}(f, y) = \begin{cases} (f - y)^2, \quad |f - y| \leq \delta \\ 2\delta |f - y| - \delta^2, \quad |f - y| > \delta \end{cases}
LHuber?(f,y)={(f?y)2,∣f?y∣≤δ2δ∣f?y∣?δ2,∣f?y∣>δ?
大多数学习算法都有参数需要设定,参数配置不同,学得模型的性能往往有显著差别,这就是通常所说的“参数调节”或简称“调参”(parameter tuning)。
模型调参和模型选择没什么本质区别:对每种参数配置都训练出模型,然后把对应最好模型的参数作为结果。这里的参数与前面所讲的参数有所不同,无法在训练过程中调整,需要用户手动去设置,这一类参数我们称之为“超参数”。
模型调参主要针对超参数进行调整,最终达到的效果是——模型在训练集上的准确性以及防止过拟合能力的大和谐,简单地说就是协调模型的偏差和方差。
网格搜索
通过查找搜索范围内的所有的点(超参数组合,超参数的笛卡尔积)来确定最优值。假设现在有三个参数年龄、性别、是否有工作:
- 年龄:低、中、高;
- 性别:男、女;
- 是否有工作:是、否;
最终所有的参数组合如下表所示:
| 序号 | 年龄 | 性别 | 是否有工作 | 序号 | 年龄 | 性别 | 是否有工作 |
|---|---|---|---|---|---|---|---|
| 1 | 低 | 男 | 是 | 7 | 中 | 女 | 是 |
| 2 | 低 | 男 | 否 | 8 | 中 | 女 | 否 |
| 3 | 低 | 女 | 是 | 9 | 高 | 男 | 是 |
| 4 | 低 | 女 | 否 | 10 | 高 | 男 | 否 |
| 5 | 中 | 男 | 是 | 11 | 高 | 女 | 是 |
| 6 | 中 | 男 | 否 | 12 | 高 | 女 | 否 |
可以看到参数组合的个数 = 年龄的取值个数 x 性别的取值个数 x 是否有工作的取值个数 = 3 x 2 x 2 = 12。如果参数的个数有 10 个,且每个参数的取值个数都为 10,那么最终参数组合个数为 10 的 10 次方。虽然网格搜索法可以找到最优的参数组合,但十分消耗计算资源和时间,特别是需要调优的超参数比较多或参数的取值个数较多。一般来说,当超参数少于四个且取值不多时,可以考虑使用网格搜索法。
【改进方案】:在实际应用中,一般会先使用较广的搜索范围和较大的步长,来寻找全局最优值可能的位置;然后逐渐缩小搜索范围和步长,来寻找更精确的最优值。
- 优点:这种方法可以降低所需的时间和计算量。
- 缺点:由于目标函数一般是非凸的,所以很可能会错过全局最优值。
我们可以使用 scikit-learn 中的 GridSearchCV 来实现对参数的评估,从而找到最优参数。
- 首先,由用户列出一个较小的超参数值域,这些超参数值域的笛卡尔集(排列组合)为一组组超参数。
- 网格搜索算法使用每组超参数训练模型,并挑选验证集误差最小的超参数组合。
关于 GridSearchCV 的更多内容请参考官方文档 传送门
【代码实现】:使用 GridSearchCV 来寻找 AdaBoost 算法的超参数。
上述案例获得的最佳参数组合恰好位于参数组合列表的边界,因此很有可能不是全局最优值,需要再做一次搜索。
最终得出最佳参数组合:{‘learning_rate’: 1, ‘n_estimators’: 50}
随机搜索
不再查搜索范围内的所有参数组合,而是在搜索范围中随机选取参数组合。具体地,随机搜索法通过固定次数的迭代(用户设定),采用随机采样分布的方式搜索合适的参数。相比网格搜索,随机搜索计算开销更小,执行速度更快,但因为是随机采样,不能保证恰好就采样到全局最优值,因此结果无法得到保证。
为什么随机搜索法的结果无法得到保证,却仍然具有应用价值呢?它的理论依据是什么?
【理论依据】:样本点集足够大,通过随机采样也能大概率地找到全局最优值,或其近似值。
我们可以使用 scikit-learn 中的 RandomizedSearchCV 类实现。关于 RandomizedSearchCV 的更多内容请参考官方文档 传送门
【代码实现】:使用 RandomizedSearchCV 来寻找 AdaBoost 算法的超参数。
通过上述代码可以看到,随机搜索法每次获得的结果都不同,且很有可能距离全局最优值很远,因此我们需要多尝试几次,最终确定全局最优值的位置。
无论是网格搜索法还是随机搜索法,都需要用户先写出参数列表,然而学习算法的很多参数都是在实数范围内取值,那么如何确定参数列表本身也成为了一个难题。
【做法 1】:对每个参数选定一个范围和变化步长,例如在先前代码示例中的 learning_rate 参数,它的取值范围在 [0, 1] 范围内。我们可以把 0.1 为步长,待评估的候选参数值设置为 5 个,则最终是从这 5 个候选值中产生选定值,即 [1, 0.9, 0.8, 0.7, 0.6]。
【做法 2】:SciPy 提供 uniform 函数,可以用于均匀随机采样,默认生成 0 与 1 之间的随机采样数值。对于 learning_rate 这一类的参数就非常使用。
贝叶斯优化
网格搜索和随机搜索在测试一个新点时,会忽略前一个点的信息;而贝叶斯优化算法则充分利用了之前的信息。贝叶斯优化算法通过对目标函数形状进行学习,找到使目标函数向全局最优值提升的参数。
具体来说,它学习目标函数形状的方法是:
- 首先根据先验分布,假设一个搜集函数;
- 然后,每一次使用新的采样点来测试目标函数时,利用这个信息来更新目标函数的先验分布;
- 最后,算法测试由后验分布给出的全局最值最可能出现的位置的点。
对于贝叶斯优化算法,有一个需要注意的地方,一旦找到了一个局部最优值,它会在该区域不断采样,所以很容易陷入局部最优值。为了弥补这个缺陷,贝叶斯优化算法会在探索和利用之间找到一个平衡点,“探索”就是在还未取样的区域获取采样点;而“利用”则是根据后验分布在最可能出现全局最值的区域进行采样。
关于贝叶斯优化更多的内容可以阅读这两篇文章:
最后,在谈谈网格搜索法、随机搜索法和贝叶斯优化三者的区别。假设现在有三个炼金术士 A、B、C,他们在探索古迹的时候找到了一篇记录如何炼制长生不老丹的书籍,里面记录了炼制的药材,但却遗漏了每份药材添加的量。这三位炼金术士耗费数年时间收集了大量的药材,于今日准备开始炼制长生不老丹。
- A 列出所有药材的所有排列组合,准备一一尝试。
- B 随机选择药材的量,希望能够撞大运炼制出不老丹。
- C 先随机选择药材的量,然后根据每次炼制后的结果进行反思。在放入5 克枸杞和当归后,炼丹炉没有发生爆炸,C 眼睛一亮,似乎 5克枸杞和当归是正确的配比,枸杞和当归的量即可固定下来,在后续的试验中可以考虑其他药材的配比。
A、B、C 的做法正好对应了网格搜索、随机搜索以及贝叶斯优化三种超参数优化方案。
- 《统计学习方法》李航
- 《百面机器学习》
- 奥卡姆剃刀原理:https://www.jianshu.com/p/533d01beb528
- 凸优化:https://www.jianshu.com/p/fe2e7f0e89e5
- 浅谈「正定矩阵」和「半正定矩阵」:https://zhuanlan.zhihu.com/p/44860862


